**Welcome! If you've ever found yourself pondering how to find the perimeter of a rectangle, or perhaps you're simply looking to refresh your memory on this fundamental geometric concept, you've landed in precisely the right place.** Whether you're a student grappling with homework, a DIY enthusiast planning a project, or just someone curious about the world around you, understanding perimeter is a valuable skill. It's not just an abstract mathematical concept; it's a practical tool that helps us measure and plan in our everyday lives. In this comprehensive article, we will embark on a detailed journey to learn how to find the perimeter of a rectangle. We'll explore the core formulas, delve into practical examples, and even touch upon real-world applications that bring this concept to life. By the end of our discussion, you'll not only grasp the "how-to" but also the "why" behind calculating the distance around any rectangular shape. ---
Table of Contents
- What Exactly is the Perimeter of a Rectangle?
- The Fundamental Formula for Perimeter: P = 2(l + w)
- Alternative Methods for Calculating Perimeter
- Step-by-Step Examples: How to Find the Perimeter of a Rectangle
- Understanding Units of Measurement
- Real-World Applications of Perimeter
- Perimeter vs. Area: A Crucial Distinction
- When to Use a Perimeter Calculator
- From Rectangles to Squares: A Special Case
- Mastering Perimeter: Tips for Students and Beyond
What Exactly is the Perimeter of a Rectangle?
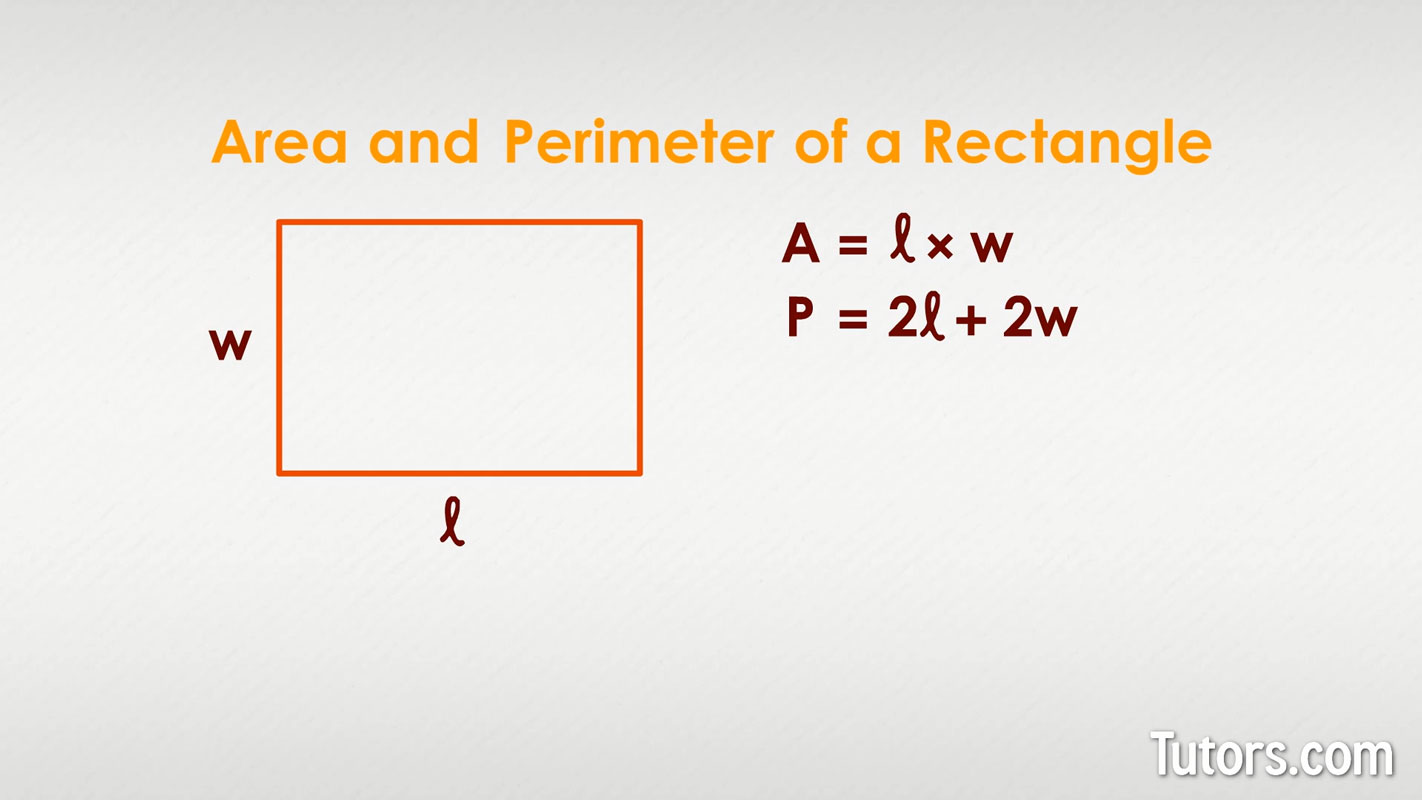
Let's begin with the basics: What is the perimeter of a rectangle? Simply put, the perimeter of a rectangle is the total distance covered around the edge of the rectangle. Imagine tracing the outline of any shape with your finger; the total path your finger travels is its perimeter. This concept applies to any shape, whether it is simple or compound. Perimeter is always the total distance around the outside edge. To truly grasp this, consider a real-world scenario. Imagine a rectangular flower garden. The perimeter of this rectangular flower garden would be the length of the fence that surrounds the garden. Or, on a larger scale, we can imagine a rectangular-shaped park with a paved sidewalk surrounding it. The perimeter of the park would be the total distance that you would have to walk to travel the complete outer distance of the park—i.e., how far you would have to walk along the sidewalk to go around the park and end up back where you started. In essence, we calculate the perimeter of a rectangle by getting the sum of all its sides.The Fundamental Formula for Perimeter: P = 2(l + w)
When it comes to how to find the perimeter of a rectangle, there's one core formula that stands out as the most efficient and widely used. This formula will help guide you as you calculate the perimeter of your own rectangle. **The basic formula for finding the perimeter of a rectangle is:** $$ P = 2 \times (l + w) $$ Here's what each part of the formula represents: * **P** stands for **Perimeter**. * **l** stands for **length** (the longer side of the rectangle). * **w** stands for **width** (the shorter side of the rectangle). In the formula for the perimeter (P) of a rectangle, 'l' is the length and 'w' is the width. This elegant formula works because a rectangle has two pairs of equal sides: two lengths and two widths. By adding the length and width together first, and then multiplying that sum by two, you are essentially accounting for all four sides. You might also see the formula written as `P = 2l + 2w`. This is the same formula written in a slightly different way, as it represents adding two lengths and two widths separately. Both expressions yield the exact same result, demonstrating the flexibility in mathematical notation. This formula is considered one of the important formulae of the rectangle, as it describes the total distance covered by the rectangle around its outside.Alternative Methods for Calculating Perimeter
While `P = 2(l + w)` is the most common and efficient way to calculate the perimeter, it's helpful to understand that there are several different ways to find the perimeter of a rectangle. You can use the one you prefer, or the one that makes the most intuitive sense to you. All these methods are based on the fundamental definition of perimeter as the sum of all sides.Adding All Four Sides Individually
The most straightforward way to find the perimeter of a rectangle is to measure all four sides of the figure and add them together. Since a rectangle has two equal lengths and two equal widths, you would simply add: $$ \text{Perimeter} = \text{length} + \text{width} + \text{length} + \text{width} $$ For instance, if you have a rectangle with a length of 6 cm and a width of 3 cm, you would calculate the perimeter as: $$ \text{Perimeter} = 6 \text{ cm} + 3 \text{ cm} + 6 \text{ cm} + 3 \text{ cm} = 18 \text{ cm} $$ This method directly reflects the definition of perimeter as the "distance around."Doubling and Adding Adjacent Sides
Another way to approach the calculation is to recognize that adjacent sides (a length and a width) sum up to half the total perimeter. So, you can add the adjacent sides and then double the answer. This is essentially what the `P = 2(l + w)` formula does. $$ \text{Perimeter} = 2 \times (\text{sum of adjacent sides}) $$ or $$ \text{Perimeter} = 2 \times (\text{length} + \text{width}) $$ This method is often preferred for its conciseness and efficiency once you understand the properties of a rectangle. It's a slightly more advanced understanding than simply adding all four sides separately, but it quickly becomes second nature.Step-by-Step Examples: How to Find the Perimeter of a Rectangle
To solidify your understanding of how to find the perimeter of a rectangle, let's walk through a few practical examples. These will illustrate the application of the formulas we've discussed.Example 1: A Simple Rectangle
Let's say you have a rectangle with a length (l) of 9 cm and a width (w) of 4 cm. **Method 1: Adding all four sides** The four sides are 9 cm, 4 cm, 9 cm, and 4 cm. $$ \text{Perimeter} = 9 \text{ cm} + 4 \text{ cm} + 9 \text{ cm} + 4 \text{ cm} = 26 \text{ cm} $$ **Method 2: Using the formula P = 2(l + w)** Here, l = 9 cm and w = 4 cm. $$ P = 2 \times (9 \text{ cm} + 4 \text{ cm}) $$ $$ P = 2 \times (13 \text{ cm}) $$ $$ P = 26 \text{ cm} $$ As you can see, both methods yield the same result, but the formula `P = 2(l + w)` allows us to calculate the perimeter of the rectangle more quickly.Example 2: Working with Decimals
Consider a rectangular piece of fabric where the length is 14.5 feet and the width is 7.5 feet. Using the formula \(perimeter=(length+width)×2\): We can see that the length is 14.5 feet and the width is 7.5 feet, so our formula becomes: $$ \text{Perimeter} = (14.5 \text{ feet} + 7.5 \text{ feet}) \times 2 $$ First, add the length and width: $$ 14.5 + 7.5 = 22.0 \text{ feet} $$ Then, multiply by 2: $$ \text{Perimeter} = 22.0 \text{ feet} \times 2 = 44 \text{ feet} $$ The perimeter of the rectangle is 44 feet.Example 3: Larger Dimensions
Imagine a large rectangular billboard with a length of 210 cm and a width of 45 cm. To find the perimeter of this rectangle, we use the formula \( p = 2(l + w) \). Substitute the values of the length and width into this equation: $$ p = 2 \times (210 \text{ cm} + 45 \text{ cm}) $$ First, sum the length and width: $$ 210 + 45 = 255 \text{ cm} $$ Then, multiply by 2: $$ p = 2 \times 255 \text{ cm} = 510 \text{ cm} $$ The perimeter of the rectangle is 510 cm. These examples clearly demonstrate the versatility and simplicity of using the perimeter formula to calculate the distance around a rectangle, regardless of the specific dimensions.Understanding Units of Measurement
When you calculate the perimeter of a rectangle, it's crucial to remember to include the units of measurement in your final answer. The units for perimeter can be any unit for the measure of length. This means whether you are calculating the perimeter using metric or imperial units, the result will always be expressed in a unit of length. Common units include: * **Metric units:** centimeters (cm), meters (m), kilometers (km) * **Imperial units:** inches (in), feet (ft), yards (yd), miles (mi) For instance, if your length and width are in "feet," your perimeter will be in "feet." If they are in "centimeters," your perimeter will be in "centimeters." Always ensure that the units for length and width are consistent before you begin your calculation. If they are not, you'll need to convert one to match the other. This attention to units ensures your answer is accurate and meaningful in a practical context.Real-World Applications of Perimeter
Understanding how to find the perimeter of a rectangle isn't just an academic exercise; it has countless practical applications in everyday life. From home improvement projects to city planning, perimeter calculations are surprisingly common. Think about these scenarios: * **Fencing a Yard or Garden:** As mentioned earlier, if you want to put a fence around your rectangular garden, you need to calculate its perimeter to know how much fencing material to buy. * **Framing a Picture or Mirror:** To buy the right amount of framing material for a rectangular picture, you'd need its perimeter. * **Decorating a Room:** If you're putting up a border wallpaper or crown molding in a rectangular room, you'll need to know the room's perimeter to purchase enough material. * **Building a Track:** When designing a rectangular running track, engineers use perimeter calculations to determine the total distance of a lap. * **Laying Out a Field:** For sports fields like football or soccer pitches, which are often rectangular, the perimeter helps in marking boundaries or planning irrigation systems. * **Sewing and Crafts:** When making a rectangular tablecloth or a quilt, knowing the perimeter helps determine the length of trim or binding needed. These examples highlight why the perimeter of a rectangle could be considered one of the important formulae. It's the total distance covered by the rectangle around its outside, making it indispensable for any task that involves outlining or enclosing a rectangular space.Perimeter vs. Area: A Crucial Distinction
While often taught together, it's vital to distinguish between perimeter and area. Both are measurements related to shapes, but they describe different aspects. * **Perimeter:** As we've extensively discussed, perimeter is the total distance around the outside edge of a shape. It's a one-dimensional measurement, expressed in units of length (e.g., meters, feet). * **Area:** Area, on the other hand, measures the amount of surface a shape covers. It's a two-dimensional measurement, expressed in square units (e.g., square meters, square feet). For a rectangle, the area is calculated by multiplying its length by its width: `Area = length × width`. For example, if a rectangle has a width of 4 inches and a height (which is another term for length in this context) of 8 inches, its area would be 4 inches × 8 inches = 32 square inches. While area and perimeter are distinct, they are both fundamental properties of a rectangle. In this article, we primarily focus on how to find the perimeter of a rectangle, but it's good to understand their differences.When to Use a Perimeter Calculator
While knowing how to calculate the perimeter manually is essential for understanding the concept, sometimes you need to estimate quickly what the perimeter of a specific rectangle is. This is where a perimeter of a rectangle calculator comes in handy. You can use our perimeter of a rectangle calculator (or any reliable online tool) if you need to quickly find the answer without manual computation. Simply enter the values for the length and width, and you'll get the result instantly. These calculators are particularly useful for: * **Quick Checks:** Verifying your manual calculations. * **Complex Numbers:** Dealing with decimals or very large numbers where manual calculation might be prone to errors. * **"What If" Scenarios:** Quickly seeing how changes in length or width affect the perimeter. * **If you know 2 values for the rectangle:** Some advanced calculators allow you to input two known values (e.g., one side length and the area, or one side length and the diagonal) and then calculate the other unknown variables, including the perimeter. While these tools are convenient, remember that understanding the underlying formulas and principles of how to find the perimeter of a rectangle is always paramount. Try to enter some values into a calculator, or read on to learn more about rectangles.From Rectangles to Squares: A Special Case
It's worth noting the relationship between rectangles and squares when discussing perimeter. A square is, in fact, a special type of rectangle where all four sides are equal in length. This means that its length and width are the same. Therefore, the formula for the perimeter of a square is a simplified version of the rectangle's formula. If 's' represents the length of one side of a square: $$ P = 2 \times (s + s) $$ $$ P = 2 \times (2s) $$ $$ P = 4s $$ To find the perimeter of a square, you simply multiply the length of one side by 4. This illustrates how mastering the concept of how to find the perimeter of a rectangle provides a foundational understanding for other geometric shapes as well.Mastering Perimeter: Tips for Students and Beyond
How does this relate to 3rd grade math and 4th grade math? Learning about perimeter is a foundational skill taught early in elementary school, building a strong base for more complex geometry later on. For young learners, visualizing the "distance around" is key. Using physical objects like books, tables, or even drawing on grid paper can make the concept tangible. For anyone looking to master how to find the perimeter of a rectangle, here are some tips: * **Visualize It:** Always imagine walking around the shape. This helps reinforce the idea of "distance around." * **Understand the Properties:** Remember that opposite sides of a rectangle are equal. This simplifies the calculation significantly. * **Practice, Practice, Practice:** The more examples you work through, the more comfortable and quick you'll become. See examples, worksheets, and calculator for practice. * **Draw Diagrams:** Sketching the rectangle and labeling its sides can help you organize your thoughts and prevent errors. * **Check Your Units:** Always ensure your final answer includes the correct unit of length. By applying these strategies, finding the perimeter of any rectangle will become second nature, empowering you with a practical skill that extends far beyond the classroom.Conclusion
We've covered a lot of ground on how to find the perimeter of a rectangle, from its basic definition to practical applications and step-by-step examples. We've learned that the perimeter is the total distance covered around the edge of the rectangle, and the most efficient way to calculate it is using the formula `P = 2 * (l + w)`, where 'l' is the length and 'w' is the width. We also explored alternative methods like adding all four sides individually or doubling the sum of adjacent sides, all of which lead to the same accurate result. Understanding perimeter is more than just a mathematical exercise; it's a valuable life skill that helps us measure, plan, and interact with the physical world around us. Whether you're a student, a professional, or simply curious, the ability to accurately calculate the perimeter of a rectangle will serve you well. Now that you're equipped with this knowledge, we encourage you to put it into practice! Try calculating the perimeter of objects around your home, or perhaps tackle some practice problems. If you have any questions, or if you'd like to share your own experiences with perimeter calculations, feel free to leave a comment below. Don't forget to share this article with anyone who might find it helpful, and explore our other guides for more insights into geometry and practical math!